Na matemática,  é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro
é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro
e diâmetro  , então aquele número é igual a
, então aquele número é igual a  . É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
. É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
 é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro
é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro
e diâmetro  , então aquele número é igual a
, então aquele número é igual a  . É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
. É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.Notação:
Os primeiros a utilizarem a letra grega  foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.
foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.
 foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.
foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica. :
:
O valor de  pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar
pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar  por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima
por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima  por 3,1415927. Para cálculos mais precisos pode-se utilizar
por 3,1415927. Para cálculos mais precisos pode-se utilizar  com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de
com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de  através de algoritmos computacionais.Um engenheiro japonês e um estudante americano de ciências da computação calcularam, usando um computador com 12 núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.
através de algoritmos computacionais.Um engenheiro japonês e um estudante americano de ciências da computação calcularam, usando um computador com 12 núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.
 pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar
pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar  por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima
por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima  por 3,1415927. Para cálculos mais precisos pode-se utilizar
por 3,1415927. Para cálculos mais precisos pode-se utilizar  com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de
com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de  através de algoritmos computacionais.Um engenheiro japonês e um estudante americano de ciências da computação calcularam, usando um computador com 12 núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.
através de algoritmos computacionais.Um engenheiro japonês e um estudante americano de ciências da computação calcularam, usando um computador com 12 núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.Aproximações para
 :
:
Desde a Antiguidade, foram encontradas várias aproximações de  para o cálculo da área do círculo.Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a
para o cálculo da área do círculo.Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a  seria
seria  , embora também seja encontrado o valor
, embora também seja encontrado o valor 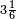 . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de  . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor
. Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor  já ser conhecido como aproximação.
já ser conhecido como aproximação.
 para o cálculo da área do círculo.Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a
para o cálculo da área do círculo.Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a  seria
seria  , embora também seja encontrado o valor
, embora também seja encontrado o valor 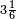 . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de  . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor
. Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor  já ser conhecido como aproximação.
já ser conhecido como aproximação.
Métodos de cálculo
Existem muitas formas de se obter o valor aproximado de  através de métodos numéricos. Consideramos que [[
através de métodos numéricos. Consideramos que [[ ]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
 através de métodos numéricos. Consideramos que [[
através de métodos numéricos. Consideramos que [[ ]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.
Método clássico para o cálculo de 
A primeira tentativa rigorosa de encontrar  deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.
deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.
 deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.
deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.
Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.
A "busca" pelo valor de  chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
 chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62.000. O resultado é aproximadamente uma circunferência de diâmetro 20.000".
Analisando matematicamente e considerando a equação citada anteriormente de  :
:
 :
:
O valor de  , portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
, portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
 , portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
, portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de  com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de
com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de  com as supracitadas 35 casas decimais.
com as supracitadas 35 casas decimais.
 com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de
com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de  com as supracitadas 35 casas decimais.
com as supracitadas 35 casas decimais.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para  .
.
 .
.
Uma aproximação de  que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
 que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:
que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:Formulação matemática do método de Arquimedes
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.
Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
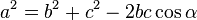
Temos formado um triângulo isósceles, de base l e lados r=1:
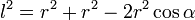
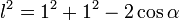


O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:

Dessa forma, o perímetro do polígono será de:

Como
 é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:
é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos: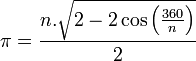
Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para:

Métodos estatísticos
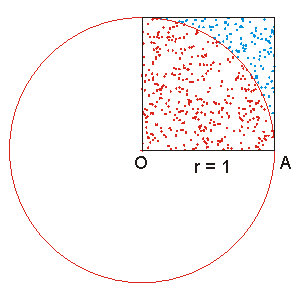
Outro método interessante para o cálculo de  pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas
pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas  e
e 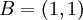 . Em seguida calcula-se a distância dos pontos sorteados
. Em seguida calcula-se a distância dos pontos sorteados 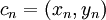 até a origem O = (0, 0).
até a origem O = (0, 0).  pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.
pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.
 pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas
pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas  e
e 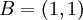 . Em seguida calcula-se a distância dos pontos sorteados
. Em seguida calcula-se a distância dos pontos sorteados 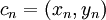 até a origem O = (0, 0).
até a origem O = (0, 0).  pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.
pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.
No exemplo ao lado , 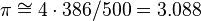
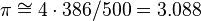
Outro método que utiliza a estatística de Monte Carlo para o cálculo de  é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.
é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.
 é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.
é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.Métodos de séries infinitas
O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de em 1593:
em 1593: .
.
 foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)=
foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)= /4.
/4. .
.
Métodos de cálculo numérico
Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função  sabemos que
sabemos que  . Os principais métodos do calculo numérico para a obtenção da raiz da função
. Os principais métodos do calculo numérico para a obtenção da raiz da função  podem incluir uma busca binária no intervalo
podem incluir uma busca binária no intervalo ![[a, b]](http://upload.wikimedia.org/wikipedia/pt/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) onde se sabemos que
onde se sabemos que 
 e
e 
 então podemos aprimorar o intervalo para:
então podemos aprimorar o intervalo para:
 sabemos que
sabemos que  . Os principais métodos do calculo numérico para a obtenção da raiz da função
. Os principais métodos do calculo numérico para a obtenção da raiz da função  podem incluir uma busca binária no intervalo
podem incluir uma busca binária no intervalo ![[a, b]](http://upload.wikimedia.org/wikipedia/pt/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) onde se sabemos que
onde se sabemos que 
 e
e 
 então podemos aprimorar o intervalo para:
então podemos aprimorar o intervalo para:-
![[a, {{a+b} \over 2}]](http://upload.wikimedia.org/wikipedia/pt/math/5/4/0/54038e4a1419787a59fba6fc401068cd.png) , se
, se 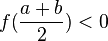 e
e
-
![[{{a+b} \over 2}, b]](http://upload.wikimedia.org/wikipedia/pt/math/9/6/1/961d4408cc3436372b070876103e77dc.png) , se
, se 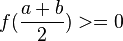
![\pi \in [3, 4]](http://upload.wikimedia.org/wikipedia/pt/math/5/c/0/5c0a97ccaab358bec9a15560fa5502a2.png) esse método permite refiná-lo sucessivamente para os intervalos
esse método permite refiná-lo sucessivamente para os intervalos
e assim sucessivamente.
Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função  utilizando um ponto inicial
utilizando um ponto inicial  exigindo que conheçamos
exigindo que conheçamos 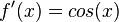 .
.
 utilizando um ponto inicial
utilizando um ponto inicial  exigindo que conheçamos
exigindo que conheçamos 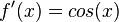 .
.
Tomando-se 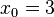 e considerando-se que por Newton-Rapson
e considerando-se que por Newton-Rapson
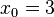 e considerando-se que por Newton-Rapson
e considerando-se que por Newton-Rapson-
 ,
,

 através das raízes de uma função pode ser obtido pela simplificação
através das raízes de uma função pode ser obtido pela simplificação-
 ,
,
 ,
,  .
.Notemos que nesses algoritmos de cálculo numérico considera-se
 como trancendental, uma vez que a função
como trancendental, uma vez que a função  não pode ser escrita através de um polinômio finito de coeficientes racionais; a função
não pode ser escrita através de um polinômio finito de coeficientes racionais; a função  é obtida através da expansão da série de Taylor.
é obtida através da expansão da série de Taylor.Grandezas que dependem de
 :
:Várias relações matemáticas dependem do conhecimento da constante
 , as mais conhecidas a nível didático são:
, as mais conhecidas a nível didático são:- Perímetro de uma circunferência:

- Área do círculo :

- Volume de uma esfera:

 também está nas fórmulas gravitacionais e do eletromagnetismo da física.
também está nas fórmulas gravitacionais e do eletromagnetismo da física.Questões sem resposta:
A questão em aberto mais importante é a de saber se  é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de
é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de  , como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.
, como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.
 é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de
é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de  , como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.
, como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.
Também não se sabe que algarismos aparecem um número infinito de vezes na constituição de  .
.
 .
.
Bailey e Crandall demonstraram em 2000 que a existência da fórmula Bailey-Borwein-Plouffe
mencionada acima e de fórmulas similares implicam a normalidade de  em base 2.
em base 2.
 em base 2.
em base 2.Cronologia do cálculo de

| Matemático | Ano | Casas Decimais |
| Egípcios (Papiro de Rhind) | 1650 A.C. | 1 |
| Arquimedes | 250 A.C. | 3 |
| Zu Chongzhi | 480 D.C. | 7 |
| Jamshid Masud Al-Kashi | 1424 | 16 |
| Ludolph van Ceulen | 1596 | 35 |
| Jurij Vega | 1794 | 126 |
| Gauss | 1824 | 200 |
| William Shanks | 1874 | 527 |
| Levi B. Smith, John W. Wrench | 1949 | 1.120 |
| Daniel Shanks, John W. Wrench | 1961 | 100.265 |
| Jean Guilloud, M. Bouyer | 1973 | 1.000.000 |
| Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura | 1982 | 16.777.206 |
| Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo | 1987 | 134.217.700 |
| Chudnovskys | 1989 | 1.011.196.691 |
| Yasumasa Kanada, Daisuke Takahashi | 1997 | 51.539.600.000 |
| Yasumasa Kanada, Daisuke Takahashi | 1999 | 206.158.430.000 |
| Yasumasa Kanada | 2002 | 1.241.100.000.000 |
| Daisuke Takahashi | 2009 | 2.576.980.370.000 |
| Fabrice Bellard | 2010 | 2.699.999.990.000 |
| Shigeru Kondo & Alexander Yee | 2010/08/02 | 5.000.000.000.000 |
| Shigeru Kondo & Alexander Yee | 2011 | 10.000.000.000.000 |

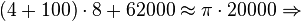



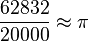



![\pi \in [3, 3.5]](http://upload.wikimedia.org/wikipedia/pt/math/2/3/8/238996635809270862ab2383deee77d5.png)
![\pi \in [3, 3.25]](http://upload.wikimedia.org/wikipedia/pt/math/6/c/8/6c886c5cc20f48284c9417fb4ecf6864.png)
![\pi \in [3.125, 3.25]](http://upload.wikimedia.org/wikipedia/pt/math/3/5/1/3516956016d85ced87e5cb01becc1b41.png)
![\pi \in [3.125, 3.1875]](http://upload.wikimedia.org/wikipedia/pt/math/0/9/c/09cb9699db5827df881ed3e4afcebde8.png)
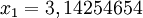

3 comentários:
Colega de faculdade Max
Sou professora da rede estadual pública e o livro desse ano foi um dos melhores que ja pude ler.
Leciono ensino médio e me deparei com o assunto Conjuntos, agora dado no 1o ano.
Estou tentando entender aqui esta questão que fala da regra ou lei de formação dos conjuntos:
Escreva, por meio de uma regra de formação, os conjuntos a seguir:
Letra C:
C = {1, 2, 4, 8,16} Resposta: C = {dois elevado a x, tal que x é um número natural menor que 5} A resposta do manual do professor é essa também, sendo que não consegui encontrar a lógica dessa resposta.Gostaria que o colega me ajudasse nisso, pois ja olhei outros livros e penso que a resposta esteja errada.Aguardo.
Olá Amiga da área de Matemática!ai´vai a resposta a sua indagação :
REPRESENTAÇÂO DOS CONJUNTOS
Os conjuntos são representados por letras maiúsculas e os elementos do mesmo são representados entre chaves. Assim, teríamos:
O conjunto das letras do nosso alfabeto; L= {a, b, c, d,..., z}.
O conjunto dos dias da semana: S= {segunda, terça,... domingo}.
A representação de conjuntos pode ser feita de três maneiras:
1º - Por extensão
Um conjunto pode ser descrito por extensão: quando o número dos seus elementos for finito e suficientemente pequeno enumerando explicitamente todos os seus elementos colocados entre chaves e separados por vírgulas.
Exemplos:
A = {Janeiro, Fevereiro, Março, Abril,..., Novembro, Dezembro} - Conjunto dos meses do ano.
V = {a, e, i, o, u} - Conjunto das vogais.
P = {2, 4, 6, 8, 10, 12,…} Conjunto dos números pares positivos.
2º - Por compreensão:
Um conjunto é representado por compreensão quando: é enunciada uma propriedade característica dos seus elementos. Isto é, uma propriedade que os seus e só os seus elementos possuam.
Exemplos:
B(meses do ano)
C= {letras do alfabeto}
D= {os meus CDs de música}
P = {p ∊ N: p = 2q para algum q ∊ N}
Q = {x ∊ N: x é primo}
R = {x: x é um número natural par e positivo}
3º - Por diagramas (veja diagramas de Venn)
Conjunto unitário
É o conjunto que possui um único elemento. Assim, teríamos:
A= {fevereiro}, B = {Número primo que é par}.
O que nos interessa é a representação Por compreensão, pois o conjunto em questão,C = {1, 2, 4, 8,16} pode ser representado pela propriedade descrita ,C = {dois elevado a x, tal que x é um número natural menor que 5} ,se considerarmos os números naturais menores que 5, que atenda a essa propriedade,poderemos enumerar todos os elementos do conjunto C,Veja: 20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
Ratificando: 2 elevado a zero é igual a 1;2 elevadoa 1 é igual a 2;2 elevado a 2 é igual a 4;2 elevado a 3 é igual a 8 é 2 elevado a 4 é igual a 16.
Postar um comentário